[SHENGTON]

I have a question about Hard disk. Have you notice that everytime we partition a Hard disk if you have 80GB the size only shows 78GB, have you guys noticed that?

So wheres the 2GB?

[Advertisements]

decimal and binary

Storage devices however are where the real confusion comes in. Some companies and software packages use binary megabytes and gigabytes, and some use decimal megabytes and gigabytes. What's worse is that the percentage discrepancy between the decimal and binary measures increases as the numbers get larger: there is only a 2.4% difference between a decimal and a binary kilobyte, which isn't that big of a deal. However, this increases to around a 5% difference for megabytes, and around 7.5% for gigabytes, which is actually fairly significant. This is why with today's larger hard disks, more people are starting to notice the difference between the two measures. Hard disk capacities are always stated in decimal gigabytes, while most software uses binary. So, someone will buy a "30 GB hard disk", partition and format it, and then be told by Windows that the disk is "27.94 gigabytes" and wonder "where the other 2 gigabytes went". Well, the disk is 27.94 gigabytes--27.94 binary gigabytes. The 2 gigabytes didn't go anywhere

[peter99]

decimal and binary

Storage devices however are where the real confusion comes in. Some companies and software packages use binary megabytes and gigabytes, and some use decimal megabytes and gigabytes. What's worse is that the percentage discrepancy between the decimal and binary measures increases as the numbers get larger: there is only a 2.4% difference between a decimal and a binary kilobyte, which isn't that big of a deal. However, this increases to around a 5% difference for megabytes, and around 7.5% for gigabytes, which is actually fairly significant. This is why with today's larger hard disks, more people are starting to notice the difference between the two measures. Hard disk capacities are always stated in decimal gigabytes, while most software uses binary. So, someone will buy a "30 GB hard disk", partition and format it, and then be told by Windows that the disk is "27.94 gigabytes" and wonder "where the other 2 gigabytes went". Well, the disk is 27.94 gigabytes--27.94 binary gigabytes. The 2 gigabytes didn't go anywhere

[vally]

There is anothe thing.
A hard drive tat has the size on it is the actual size in gigabyte (I do not think it is percentage.)
When you format a disk to use it there is some space beaing used to set the format of the disk ntfs/fat32...
Different manufacturers that sell the same size disk but in reality they may not have the exact same amount of free space. I once had 2 disk one by Kingston the other WD both were 200gig but after being formated they had a 8 gig difference.

[SHENGTON]

Just confusing about the 80GB in Windows the hard drive read 78GB then from the picture, the 80GB is only 74GB. So what happen to the 4GB? what's the correct computation of this?

[peter99]

If you want to work out the capacity for large hard drives in windows do this calculation

ie 80 gig drive

80000 divide by 1073 = 74.55 gig

[SHENGTON]

Thanks sir but my question is why Windows show 78GB? if trying to calculate that it's only 74GB.

Edited by SHENGTON, 12 October 2007 - 07:47 AM.

[peter99]

Binary vs. Decimal Measurements

One of the most confusing problems regarding PC statistics and measurements is the fact that the computing world has two different definitions for most of its measurement terms. :^) Capacity measurements are usually expressed in kilobytes (thousands of bytes), in megabytes (millions of bytes), or gigabytes (billions of bytes). Due to a mathematical coincidence, however, there are two different meanings for each of these measures.

Computers are digital and store data using binary numbers, or powers of two, while humans normally use decimal numbers, expressed as powers of ten. As it turns out, two to the tenth power, 2^10, is 1,024, which is very close in value to 1,000 (10^3). Similarly, 2^20 is 1,048,576, which is approximately 1,000,000 (10^6), and 2^30 is 1,073,741,824, close to 1,000,000,000 (10^9). When computers and binary numbers first began to be used regularly, computer scientists noticed this similarity, and for convenience, "hijacked" the abbreviations normally used for decimal numbers and began applying them to binary numbers. Thus, 2^10 was given the prefix "kilo", 2^20 was called "mega", and 2^30 "giga".

This shorthand worked fairly well when used only by technicians who worked regularly with computers; they knew what they were talking about, and nobody else really cared. Over the years however, computers have become mainstream, and the dual notation has led to quite a bit of confusion and inconsistency. In many areas of the PC, only binary measures are used. For example, "64 MB of system RAM" always means 64 times 1,048,576 bytes of RAM, never 64,000,000. In other areas, only decimal measures are found--a "28.8K modem" works at a maximum speed of 28,800 bits per second, not 29,491.

Storage devices however are where the real confusion comes in. Some companies and software packages use binary megabytes and gigabytes, and some use decimal megabytes and gigabytes. What's worse is that the percentage discrepancy between the decimal and binary measures increases as the numbers get larger: there is only a 2.4% difference between a decimal and a binary kilobyte, which isn't that big of a deal. However, this increases to around a 5% difference for megabytes, and around 7.5% for gigabytes, which is actually fairly significant. This is why with today's larger hard disks, more people are starting to notice the difference between the two measures. Hard disk capacities are always stated in decimal gigabytes, while most software uses binary. So, someone will buy a "30 GB hard disk", partition and format it, and then be told by Windows that the disk is "27.94 gigabytes" and wonder "where the other 2 gigabytes went". Well, the disk is 27.94 gigabytes--27.94 binary gigabytes. The 2 gigabytes didn't go anywhere.

Another thing to be careful of is converting between binary gigabytes and binary megabytes. Decimal gigabytes and megabytes differ by a factor of 1,000 but of course the binary measures differ by 1,024. So this same 30 GB hard disk is 30,000 MB in decimal terms. But its 27.94 binary gigabytes are equal to 28,610 binary megabytes (27.94 times 1,024).

One final "gotcha" in this area is related to arithmetic done between units that have different definitions of "mega" or "giga". For example: most people would say that the PCI bus has a maximum theoretical bandwidth of 133.3 Mbytes/second, because it is 4 bytes wide and runs at 33.3 MHz. The problem here is that the "M" in "MHz" is 1,000,000; but the "M" in "Mbytes/second" is 1,048,576. So the bandwidth of the PCI bus is more properly stated as 127.2 Mbytes/second (4 times 33,333,333 divided by 1,048,576).

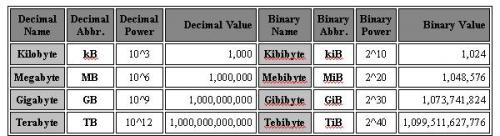
There's potential good news regarding this whole binary/decimal conundrum. The IEEE has proposed a new naming convention for the binary numbers, to hopefully eliminate some of the confusion. Under this proposal, for binary numbers the third and fourth letters in the prefix are changed to "bi", so "mega" becomes "mebi" for example. Thus, one megabyte would be 10^6 bytes, but one mebibyte would be 2^20 bytes. The abbreviation would become "1 MiB" instead of "1 MB". "Mebibyte" sounds goofy, but hey, I'm sure "byte" did too, 30 years ago. ;^) Here's a summary table showing the decimal and binary measurements and their abbreviations and values ("bytes" are shown as an example unit here, but the prefices could apply to any unit of measure):


http://www.pcguide.c.../fun/bindec.htm

Attached Thumbnails

• 

Edited by peter99, 12 October 2007 - 09:22 AM.