Hi Japstar,
You did'nt mention the no. of squares that must be displayed so I will be assuming that its a user input.
The logic I thought was to consider only one side of the square, rotate it around the Co-ordiante axis, and draw the rest of the 3 lines of the square relative to it.
I'll be rotating the the side of the square around (0,0). And angle between two squares will depend on the no. of squares the user has asked to display.
Below is the list of variables I'll be using:
l: Is the length of the side of the square
i: The index variable to increment the angle.
angle: The angle calculated according to the no. of squares the user want to display.
x: The x co-ordinate of the other end of the first line.
y: The y co-ordinate of the other end of the first line.
n: The no. of squares the user want on the screen.
I'll illustrate two iterations of the logic with a diagram(pls. excuse the quality of the fig.; I suck at drawing), refer the fig. below:
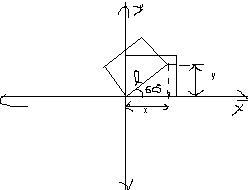
Initially our line under consideration is drawn a 0degrees, the rest of square is built on basis of it. In this e.g. I will take
angle as 60degrees. I tilt our main line by 60dgs; now all we have to do is find the co-ordinates (
x,
y) to draw our main line. This can obtained from the formulae below:
x=l*cos(60)
y=l*sin(60)
The rest of the square can be built on basis of it.
i=0
angle = 360/n
while(i<360)
{
x = l*cos(angle)
y = l*sin(angle)
line(0,0,x,y); //the lib. function to draw a line
//this is only to draw the first line, I leave the rest of the lines to you
line(__ , __ , __ , ___)
line(__ , __ , __ , ___)
line(__ , __ , __ , ___)
i+=angle
}
Note if you intend to implement this code on a actual PC: The computer screen only has the 4th-quadrant of the co-ordinate system; so you will have to take an arbitary origin.
Edited by darth_ash, 05 March 2006 - 09:41 AM.

















 Sign In
Sign In Create Account
Create Account

